Mentalidad de los mejores científicos informáticos

La primera vez que tomé una clase con el profesor del MIT Eric Grimson, quedé impresionado. La mentalidad de los mejores programadores y científicos informáticos tiene una forma completamente diferente de ver el mundo, una perspectiva totalmente crítica y algorítmica. Pero, ¿cuál es la característica que realmente distingue a un programador novato de un programador de élite? Bueno,

Pensamiento computacional.

A la lectura, escritura y aritmética, debemos agregar el pensamiento computacional en la habilidad analítica de cada niño

• Jeannette Wing

¿Qué es el pensamiento computacional?

El Pensamiento computacional (CT) puede entenderse como una forma alternativa de pensar relacionada con la aparición de las computadoras, ya que crea un entorno cognitivo donde se unen el pensamiento lógico de ingeniería, científico y matemático (Wing, 2008).

El pensamiento computacional se basa en una serie de conceptos derivados de la ciencia de la computación. Por ejemplo, según la Sociedad Internacional para la Tecnología en la Educación (ISTE, 2011), el pensamiento computacional se define como un proceso de resolución de problemas que abarca las siguientes características, entre otras:

• Formular problemas de manera que permita el uso de computadoras y otras herramientas para trabajar hacia su solución.
• Organizar y analizar datos lógicamente.
• Representar datos de manera abstracta a través de modelos y simulaciones.
• Automatizar soluciones mediante el pensamiento algorítmico, basado en una serie de pasos ordenados.
• Identificar, analizar e implementar posibles soluciones para encontrar la combinación de pasos y recursos de manera más eficiente y efectiva.
• Generalizar y transferir este proceso de resolución de problemas a otros problemas.

Además, las actividades que promueven el pensamiento computacional fomentan el desarrollo de diversas habilidades específicas en las personas, que incluyen:

• Confianza para lidiar con la complejidad.
• Persistencia en el trabajo con problemas desafiantes.
• Tolerancia a la ambigüedad.
• Capacidad para abordar problemas abiertos y cerrados.
• Capacidad para comunicarse y colaborar con otros para lograr un objetivo común.

¡Intentemos algo!

Considera el siguiente problema y explora diversas estrategias para encontrar una solución efectiva: ¿Cómo abordarías la tarea de calcular la raíz cuadrada de un número, al que llamaremos ‘n’? Este desafío no solo nos invita a realizar una operación matemática fundamental, sino que también fomenta la aplicación de diferentes enfoques y técnicas para llegar a una solución eficiente. Podríamos comenzar explorando métodos algebraicos tradicionales, como factorizar ‘n’ o buscar factores cuadrados perfectos, pero también podríamos aplicar métodos sofisticados como la identidad exponencial, las aproximaciones de Bakhshali, la serie de Taylor, etc.

Pero, ¿cuál método es el más efectivo? - Una pequeña broma: como solía decir mi profesor de matemáticas de la escuela secundaria, “Saca la calculadora”. - La cuestión es que, para calcular la raíz cuadrada, necesitarías un algoritmo para resolverlo. Aquí es donde entra en juego el pensamiento algorítmico, capaz primero de entender el problema y luego encontrar la solución óptima. Podemos definir el pensamiento algorítmico como la capacidad de pensar en términos de secuencias y reglas que sirven para resolver problemas (CAS, 2015).

Quizás pienses en calcular la raíz cuadrada como encontrar dos números que, cuando se multiplican entre sí, dan como resultado “n”. Comenzando, por ejemplo, con n = 9, con un algoritmo como el siguiente:

• 1x1=1
• 2x2=4
• 3x3=9

¡Lo hiciste! Encontraste la raíz cuadrada de 9 (3). Pero ahora, consideremos n = 841. Los pasos del algoritmo se incrementan a 29. Si bien este es un algoritmo simple, fácil y práctico, se vuelve menos escalable a medida que los números crecen más. Otro problema: solo encuentra raíces cuadradas perfectas, lo que significa que sería incapaz de encontrar la raíz cuadrada de 8 (2.82842712475). En la ciencia de la computación, el trabajo de los científicos se centra en encontrar los algoritmos más eficientes. Es decir, aquellos que resuelven un problema utilizando la menor cantidad de recursos posibles (memoria, comunicaciones, tiempo de procesamiento, etc.) de la manera más efectiva al proporcionar la respuesta correcta o la aproximación más cercana a ella.

En este sentido, este algoritmo no sería muy útil. Aquí tienes un ejemplo de cómo implementar este algoritmo en Python:

def raiz_cuadrada(numero):
    for i in range(1, numero + 1):
        if i * i == numero:
            print(f'La raíz cuadrada de {numero} es {i}')
            return  # Salir de la función una vez que se encuentre la raíz cuadrada
    print(f'El número {numero} no tiene una raíz cuadrada perfecta')

if __name__ == '__main__':
    numero = int(input("¿Cuál es el número para encontrar la raíz cuadrada? "))
    raiz_cuadrada(numero)

Puedes ver el repositorio de Github con los algoritmos aquí

Con el algoritmo anterior, debemos entender que cuanto mayor sea el número para el que buscamos la raíz cuadrada, mayor será el tiempo de ejecución, ya que este algoritmo crece linealmente con la entrada proporcionada. En otras palabras, si estamos buscando la raíz cuadrada del número 287296, el bucle repetiría la acción 536 veces.

En el campo de la ciencia de la computación, la eficiencia de un algoritmo a menudo se mide mediante la complejidad algorítmica, que cuantifica cómo cambia el tiempo de ejecución o el uso de recursos a medida que cambia el tamaño de la entrada. La notación Big O, representada como O(f(n)), es una herramienta comúnmente utilizada para describir esta complejidad.

Raíces cuadradas no perfectas

Hasta este punto, hemos estado pensando como humanos que buscan resolver problemas complejos, ¡pero tenemos computadoras súper potentes, verdad? ¿Por qué no incrementamos el número en decimales para ver si podemos encontrar la raíz cuadrada de esa manera? En otras palabras, hagamos una búsqueda aumentando en 0.1, como 1.1 * 1.1, 1.2 * 1.2, y así sucesivamente.

Codifiquemos

def raiz_cuadrada(numero):
    """
    Calcular la raíz cuadrada aproximada de un número dado utilizando el método iterativo.

    Parámetros:
    - numero (float): El número para el cual se calculará la raíz cuadrada.

    Retorna:
    - None: Imprime la raíz cuadrada aproximada si se encuentra; de lo contrario, indica que el número
      no tiene una raíz cuadrada perfecta.
    """
    suposicion = 1.0

    # Iterar hasta que el cuadrado de la suposición esté lo suficientemente cerca del número objetivo
    while (suposicion * suposicion) < numero:
        suposicion += 0.00000001

        # Comprobar si la suposición está lo suficientemente cerca de la raíz cuadrada
        if abs(suposicion * suposicion - numero) < 0.0001:  
            print(f'La raíz cuadrada de {numero} es aproximadamente {suposicion}')
            return
    
    # Si el bucle se completa sin encontrar una raíz cuadrada lo suficientemente cercana
    print(f'El número {numero} no tiene una raíz cuadrada perfecta')

if __name__ == '__main__':
    # Obtener la entrada del usuario para el número
    numero = float(input("¿Cuál es el número para encontrar la raíz cuadrada? "))
    
    # Llamar a la función raiz_cuadrada con el número proporcionado
    raiz_cuadrada(numero)

A pesar de que el código proporcionado anteriormente demuestra la capacidad de calcular con precisión raíces cuadradas no perfectas, surge una limitación significativa: su ineficiencia, incluso en el contexto de sistemas informáticos de alta capacidad. Aunque la ejecución del algoritmo puede haber sido tolerable para valores de raíz cuadrada no perfectos como 2, 3 o 5, surge la necesidad de examinar más de cerca la naturaleza subyacente del problema.

El algoritmo comienza con la variable en el valor de 1 y la incrementa en pasos de 0.00000001 en cada iteración. En consecuencia, en la primera iteración, la variable toma el valor de 1.00000001, y se requieren diez iteraciones adicionales para alcanzar 1.00000010. Este patrón revela la progresión gradual del valor de la variable a medida que se acerca al número deseado. Para determinar el número de iteraciones requeridas, se puede emplear la siguiente expresión matemática.

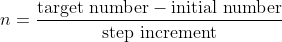
En el escenario actual, al ejecutar el algoritmo para determinar la raíz cuadrada de 3, el resultado obtenido es 1.7320239455511578. Aplicando la fórmula matemática destinada a determinar el número de iteraciones requeridas para lograr este resultado, se obtiene el siguiente valor.

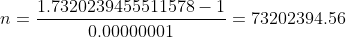
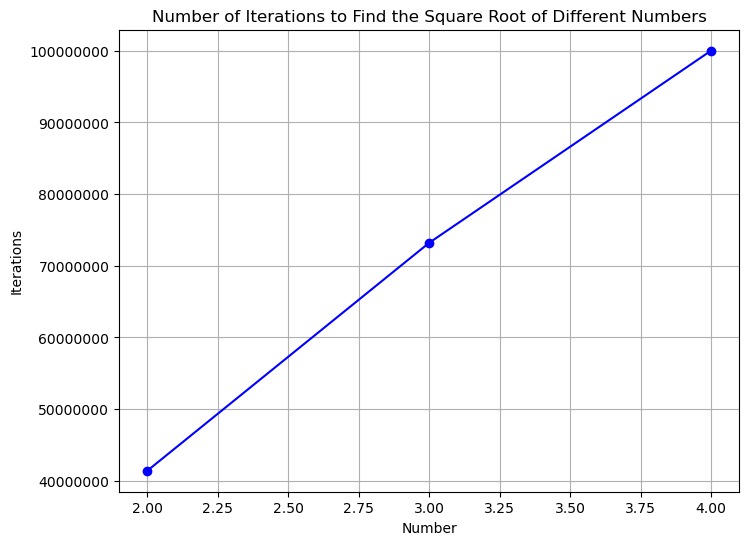
Si bien este enfoque puede ser viable para raíces cuadradas no perfectas de magnitudes más pequeñas, es crucial considerar la magnitud del número requerido de iteraciones y el costo computacional consiguiente al aplicar este algoritmo a valores considerablemente más grandes, como se ilustra en el caso de la raíz cuadrada de 287294. La complejidad resultante podría plantear un desafío computacional significativo.

Se adjunta un gráfico que visualiza el costo computacional asociado con la determinación de la raíz cuadrada para números del 1 al 4. Esta representación gráfica tiene como objetivo proporcionar una perspectiva clara sobre la ineficiencia de implementar este algoritmo, especialmente cuando se enfrenta a valores numéricos más grandes.

¡Te toca a ti!

Hemos observado que, aunque este método puede considerarse “simple” en su aplicación mínima para los humanos, carece de la eficiencia necesaria para abordar problemas más complejos en el contexto de las capacidades computacionales. Ahora es el momento de aprovechar el formidable poder del pensamiento computacional e intentar concebir una solución más óptima. Te animo a que enfrentes el desafío y reflexiones sobre una estrategia que pueda mejorar la eficiencia del algoritmo propuesto.

Te presento una cita de Richard Feynman, un distinguido físico y una de mis figuras preferidas en el campo, sobre la resolución de algoritmos. Si no logras encontrar una solución, no te preocupes; sigamos nuestro proceso de aprendizaje juntos.

Identidad exponencial

Estamos acostumbrados a denotar la raíz cuadrada de la siguiente manera:

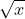
Sin embargo, podemos expresar la raíz cuadrada de cualquier número utilizando la identidad exponencial elevando ese número a la potencia de 1/2.

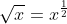
¿Bajo esta lógica, podemos obtener fácilmente la raíz cuadrada de cualquier número de manera práctica y eficiente? Intentémoslo.

def calcular_raiz_cuadrada(identidad_exponencial):
    """
    Calcular la raíz cuadrada utilizando la identidad exponencial.

    Parámetros:
    - identidad_exponencial (float): Número para el cual se calculará la raíz cuadrada.

    Retorna:
    - float: Resultado de la raíz cuadrada.
    """
    resultado_raiz_cuadrada = identidad_exponencial ** 0.5
    return resultado_raiz_cuadrada

if __name__ == "__main__":
    # Ejemplo de uso
    numero = 25
    resultado = calcular_raiz_cuadrada(numero)
    print(f"La raíz cuadrada de {numero} es: {resultado}")

¿Lo logramos? ¿Hemos encontrado el algoritmo perfecto para encontrar la raíz cuadrada? Aunque este pueda ser un algoritmo simple y fácilmente implementable con requisitos de recursos computacionales relativamente bajos, necesitamos examinar su funcionamiento en detalle para determinar si es lo suficientemente hábil.

• Simplicidad: No necesitamos preocuparnos por algoritmos complejos, ya que esta implementación es una solución directa que no requiere iteraciones.

• Eficiencia: Este algoritmo podría resolver el problema en mucho menos tiempo que otros tipos de algoritmos iterativos que requieren una gran potencia informática. Dado que el algoritmo implica solo una operación principal sin bucles o recursión, su complejidad permanece constante independientemente del tamaño de la entrada.

En términos de notación de complejidad, esto se expresa como O(1), lo que significa que la complejidad del algoritmo no aumenta con el tamaño de la entrada. Este tipo de complejidad es ideal y refleja un rendimiento constante, haciendo que el algoritmo sea eficiente para calcular la raíz cuadrada de un solo número.

• Precisión: Para la mayoría de los casos prácticos o cotidianos, este algoritmo podría tener una precisión completamente aceptable, proporcionando un número razonable de decimales para situaciones de la vida diaria.

Pero ¿serviría para un problema matemático o científico?

• Limitado a Valores Reales Positivos: Este método funciona bien para números reales positivos, pero no es directamente aplicable a números complejos o valores negativos. En tales casos, se necesitarían consideraciones adicionales.

• Precisión Limitada para Números Grandes o Pequeños: Para números extremadamente grandes o pequeños, este método puede experimentar problemas de precisión. Los números de punto flotante de Python tienen límites en su precisión, lo que puede afectar la precisión del resultado.

• No Aborda Completamente la Ineficiencia para Ciertos Valores: Aunque es más eficiente que algunos métodos iterativos, aún puede no ser lo suficientemente eficiente para valores extremadamente grandes debido a las limitaciones de la aritmética en punto flotante.

El método de identidad exponencial es una opción simple y eficiente para calcular la raíz cuadrada, especialmente para números reales positivos en situaciones donde la precisión no es crítica. Sin embargo, es importante tener en cuenta sus limitaciones, especialmente al trabajar con valores extremadamente grandes o pequeños. Para aplicaciones que requieren mayor precisión o necesitan manejar números complejos o negativos, podrían ser necesarios enfoques más avanzados.

Un viaje a través del tiempo

En las antiguas tierras de Babilonia, entre los ríos Éufrates y Tigris, floreció una civilización, dejando un valioso legado matemático. En medio de sus logros en arquitectura, astronomía y comercio, los babilonios también desarrollaron ingeniosos métodos para abordar problemas numéricos, incluida la búsqueda de soluciones para las raíces cuadradas.

Se cree que hace más de 4.000 años, los babilonios emplearon la noción de raíces cuadradas en el contexto práctico de la medición de tierras y la construcción. Aunque no formalizaron teoremas en términos modernos, su comprensión se manifestó en su capacidad para resolver problemas geométricos y encontrar las longitudes de los lados de cuadrados.

En este escenario, los babilonios desarrollaron un método iterativo que llegaría a conocerse como el Método Babilónico o Método de Herón. Aunque sus registros escritos no han sobrevivido en detalle, se sabe que utilizaron aproximaciones sucesivas para encontrar raíces cuadradas.

El Método Babilónico, con su base geométrica y práctica, refleja la ingeniería matemática de una civilización que utilizaba herramientas numéricas para comprender y dar forma a su entorno. Aunque su legado se ha fundido con el polvo del tiempo, el Método Babilónico persiste como precursor de los métodos numéricos que se desarrollarían a lo largo de la historia, y su influencia resonaría en la rica sinfonía del progreso matemático y científico.

El Método Babilónico, también conocido como Método de Herón, es un enfoque iterativo para calcular raíces cuadradas. Aunque su desarrollo original se atribuye a los babilonios, es más conocido por la descripción de Herón de Alejandría. Aquí hay una explicación semi-formal del algoritmo:

1. Elección de la Aproximación Inicial (A): Comience con una estimación inicial A. Puede ser cualquier número que crea que está cerca de la raíz cuadrada del número que desea calcular.

2. Iteración: Utilice la siguiente fórmula iterativa para mejorar la aproximación en cada paso:

Repetición: Repita el paso 2 hasta que la aproximación (A_{n+1}) esté lo suficientemente cerca de (A_n) o hasta que alcance un número predefinido de iteraciones.

El proceso se repite varias veces, y en cada iteración, la aproximación se ajusta para acercarse cada vez más a la raíz cuadrada verdadera. La fórmula utiliza la estimación

anterior y el número original para generar una nueva estimación que se espera que esté más cerca de la raíz cuadrada.

Veamos un ejemplo:

Tomemos el número 100 como ejemplo y tratemos de calcular su raíz cuadrada utilizando el Método Babilónico.

1. Elección de la Aproximación Inicial (A): Podemos comenzar con cualquier estimación inicial. Tomemos la mitad del número como nuestra primera aproximación. Entonces, (A = 100 / 2 = 50).

2. Iteración: Usemos la fórmula iterativa para mejorar nuestra aproximación:

[ A_{n+1} = \frac{1}{2}(A_n + \frac{S}{A_n}) ]

Donde (S) es el número original (en nuestro caso, 100) y (A_n) es nuestra estimación actual.

Para la primera iteración:

[ A_1 = \frac{1}{2}(50 + \frac{100}{50}) = \frac{1}{2}(50 + 2) = \frac{1}{2} \cdot 52 = 26 ]

Para la segunda iteración:

[ A_2 = \frac{1}{2}(26 + \frac{100}{26}) ]

Repitiendo este proceso varias veces, eventualmente llegamos a una estimación que es lo suficientemente cercana a la raíz cuadrada verdadera del número original.

Este método es notable por su eficiencia y su capacidad para generar resultados precisos en un número relativamente pequeño de iteraciones. Es un ejemplo clásico de la aplicación del pensamiento computacional en la resolución de problemas numéricos.

---

Conclusión

El Pensamiento computacional es una habilidad esencial en el arsenal de cualquier científico informático o programador, y su aplicación puede extenderse a una amplia gama de dominios y disciplinas. Desde el diseño de algoritmos hasta la resolución de problemas complejos, el pensamiento computacional proporciona un marco para abordar desafíos de manera estructurada y eficiente.

En el contexto específico de la búsqueda de raíces cuadradas, hemos explorado varios enfoques, desde métodos simples y directos hasta algoritmos más sofisticados y eficientes. A través de este viaje, hemos demostrado cómo el pensamiento computacional puede guiar el desarrollo y la evaluación de soluciones, teniendo en cuenta consideraciones de simplicidad, eficiencia y precisión.

Aunque hemos llegado a una comprensión más profunda de estos métodos y sus aplicaciones, nuestro viaje no ha terminado. Como estudiantes y practicantes de la ciencia de la computación, siempre habrá nuevos desafíos que abordar y nuevas soluciones que descubrir. Con el poder del pensamiento computacional a nuestro lado, estamos equipados para enfrentar estos desafíos con confianza y creatividad.

¡Sigamos explorando, aprendiendo y creando juntos en nuestro viaje hacia el dominio del mundo digital!

---

Referencias

• CAS (Computing at School). (2015). Computational Thinking: A guide for teachers. Recuperado de https://www.computingatschool.org.uk/data/uploads/ComputationalThinking.pdf

• ISTE (International Society for Technology in Education). (2011). National Educational Technology Standards and Performance Indicators for Students. Recuperado de https://www.iste.org/standards/for-students

• Wing, J. (2008). Computational Thinking and Thinking About Computing. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 366(1881), 3717–3725. https://doi.org/10.1098/rsta.2008.0118

• Solomon, J. (2017). Algoritmos en python: teoría y práctica. Recuperado de https://books.google.co.ve/books?id=19A-DwAAQBAJ

• Brown, R. (2018). Fundamentos de Python: Primeros pasos con la programación y la ciencia de datos. Recuperado de https://books.google.co.ve/books?id=pBpxDwAAQBAJ